Background

This blog post discusses the reasoning process I went through while addressing a particular problem in entity matching. Although libraries exist to address this task, my focus here is on the conceptual questions that arise during problem solving.

Entity Ambiguity

In principle, entity matching should not involve ambiguity. Ambiguity may occur in relations (triplets), but not in the entities themselves. The following discussion focuses on the notion of semantic ambiguity.

Consider three entities, $e_1$, $e_2$, and $e_3$. In an abstract semantic space (assuming such a space exists), suppose that $e_1$ is very close to $e_2$, and $e_2$ is similarly close to $e_3$:

        e1         e3
             e2

However, $e_1$ and $e_3$ are not close to one another. This raises the question: how should such entities be categorized, particularly in the case where $dist(e_1, e_2) = dist(e_3, e_2)$?

At first glance, this might appear to be a challenging problem. Yet, in practice, such a situation does not arise. The reason is that each entity corresponds objectively to a distinct object in reality. While multiple names may refer to the same object, they ultimately designate the same referent. Semantic similarity does not imply equivalence.

For example, consider the case of two entities whose meanings overlap semantically:

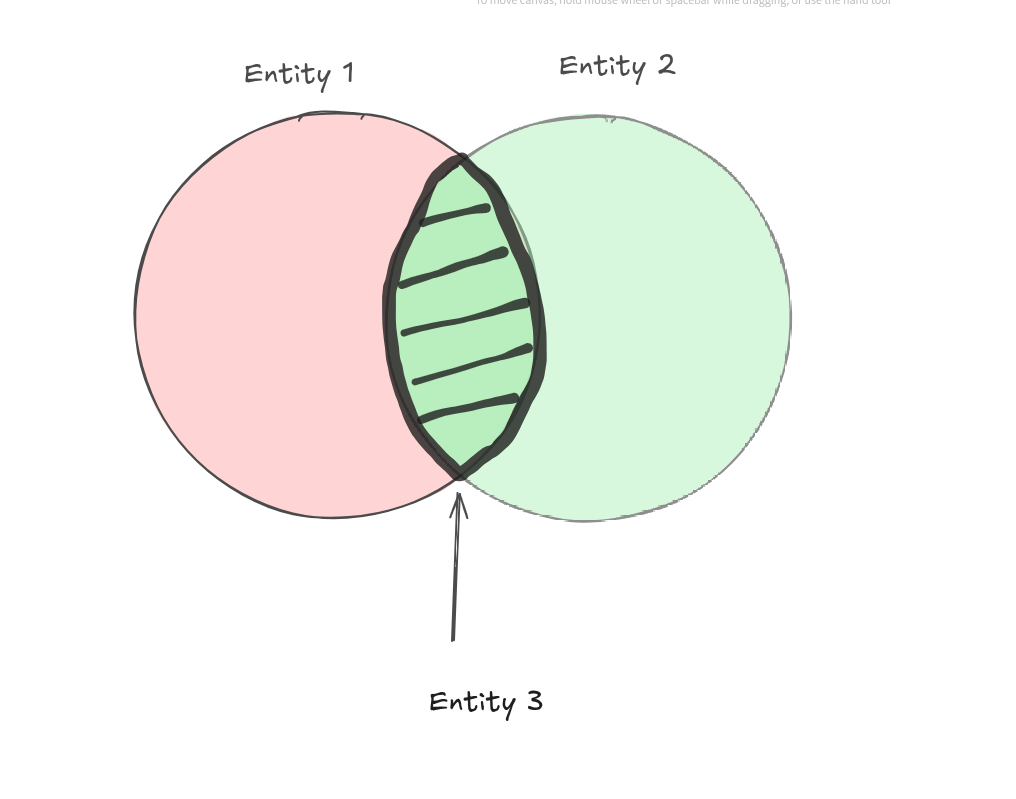
One might hypothesize the existence of a third entity that shares this overlapping feature. In such cases, these three entities should still be treated as distinct and should not be matched to one another. Why?

Because reality contains no inherently ambiguous objects. Entities that appear similar in semantic space remain distinct in the real world. A simple linguistic example illustrates this point: jelly, jellyfish, and fish. Despite partial overlap in their semantics, they denote different entities and should not be conflated.

Here’s a more formal and polished rewrite of your draft blog section. I kept the technical details intact while adjusting the tone and structure to make it more academic and polite:

Optimization

The inherent nature of the entity matching problem suggests a time complexity of $\mathcal{O}(N^2)$, which is impractical in most real-world scenarios due to computational cost and latency. For example, processing 120 entities may require more than 10,000 API calls and approximately 30 minutes of execution time.

First Attempt

The first optimization strategy relies on a strong assumption: that each entity must correspond to a concrete object in reality. For instance, terms such as dog and puppy ultimately refer to the same real-world concept. By leveraging this assumption, certain redundant comparisons can be skipped.

Consider a simple case where entities are indexed as follows:

0 1 2 3 4

A naïve pairwise comparison approach would result in the following API calls:

0 -> 1
0 -> 2
0 -> 3
0 -> 4
1 -> 2
1 -> 3
1 -> 4
...

However, if we detect early on that entity 0 and entity 1 represent the same object, then subsequent comparisons involving 1 (e.g., 1 -> 2, 1 -> 3, 1 -> 4) can be skipped. This optimization is particularly effective when duplicate or synonymous entities are detected in the early stages.

As another example, if entities 0 and 3 are equivalent, and 0 is already known to be equivalent to 1, then during the 1 iteration we only need to check 1 -> 2 and 1 -> 4; comparisons with 3 are unnecessary.

Second Attempt

The second approach applies a blocking technique, in which the dataset is partitioned into smaller subgroups. This substantially reduces the number of required comparisons, as the time complexity becomes $\mathcal{O}\bigl(\tfrac{N}{M}\bigr)^2$, where $N$ is the number of entities and $M$ is the number of subgroups.

For example, blocking can be based on semantic attributes:

data_dict = {
    '澳門': (type: 'location', definition: 'Refers to Macao, the Special Administrative Region of China and former Portuguese colony.'),
    '濠鏡澳': (type: 'location', definition: 'An ancient Chinese name for Macao, meaning "Oyster Mirror Bay".'),
    'pencil': (type: 'tool', definition: 'refers to pencil'),
    'pen': (type: 'tool', definition: 'refers to pen')
}

Here, the attribute type can be used to separate entities into groups such as location and tool, thereby eliminating unnecessary cross-category comparisons.

Third Attempt

Building on the previous strategies, asynchronous execution can further improve efficiency. Instead of sequentially querying pairs such as:

0 -> 1
0 -> 2
0 -> 3
0 -> 4
1 -> 2
1 -> 3
1 -> 4
...

the first batch of comparisons can be executed concurrently:

0 -> 1
0 -> 2
0 -> 3
0 -> 4

The results can then be used to update the disjoint set structure before proceeding with subsequent iterations.

Fourth Attempt

Instead of comparing pairs individually, we can prompt the LLM with a group of candidate entities. For example, given a main entity and five candidate entities, we may ask the LLM to identify which candidates correspond to the same meaning:

main entity: {main_entity}
entity candidates: 
1. candidate 1
2. candidate 2
...
5. candidate 5

Please list the candidates that have the same meaning as {main_entity}.

This method reduces time complexity to approximately $\mathcal{O}\bigl(\tfrac{N}{M \times C}\bigr)^2$, where $C$ is the number of candidates per query. However, this strategy may decrease accuracy, as LLM outputs are not always deterministic or reliable.

Benchmark

As mentioned, the naïve method requires around 30 minutes for 120 entities. With optimization, this time can be reduced to approximately 10 minutes. While this is a significant improvement, it remains inefficient for large-scale applications.

Alternative Approach

An alternative method is to compute semantic similarity directly, rather than querying the LLM for each pair. Although high-dimensional embeddings (e.g., text-embedding-3-small from OpenAI) may suffer from the curse of dimensionality, smaller and widely used embedding models—such as all-MiniLM-L6-v2—can often provide competitive results.

Empirically, this approach performs reasonably well, especially in domain-specific contexts (e.g., cultural terminology related to Macau). Moreover, it is substantially faster than repeated LLM queries, making it a practical option for many real-world applications.